To this end I created a Python module I can import into Python that will optimize this problem for us. From Python, I wanted to be able to send my initial guess of p, my measured data, and the x-values these measurements were taken at and have returned the parameter values as well as the optimization information. To interface with C++ from Python, I made use of the Numpy C-API. You can use Cython for this as well and it would probably be easier to implement but I haven't tried that yet. Using Microsoft's Visual Studio program I created a static library of the levmar routine in a separate project. I then reference that library in this DLL (pyd) module. My C++ code is as follows:
#include "Python.h"
#define NPY_NO_DEPRECATED_API NPY_1_7_API_VERSION
#include "arrayobject.h"
#include <iostream>
#include <iomanip>
#include <cmath>
#include <cfloat>
#include "levmar.h"
using namespace std;
struct argstruct {
double *xval;
};
double lorentz(double *p, double x) {
return p[2] / (1.0 + pow((x / p[0] - 1.0), 4) * pow(p[1], 2));
}
void lorentzfit(double *p, double *x, int m, int n, void *data) {
register int i;
struct argstruct *xp;
double xval;
xp = (struct argstruct *) data;
for(i=0; i<n i++) {
xval="xp-">xval[i];
x[i] = lorentz(p, xval);
}
}
static PyObject *levmarfit(PyObject *self, PyObject *args) {
PyArrayObject *xval, *yval, *p0, *results;
npy_intp *dimx, *dimy, *dimp;
argstruct adata;
int ndx, ndy, ndp, ret, parse_ind;
double *x, *p;
double opts[LM_OPTS_SZ] = {LM_INIT_MU, 1E-15, 1E-15, 1E-20, -LM_DIFF_DELTA};
double info[LM_INFO_SZ];
parse_ind = PyArg_ParseTuple(args, "O!O!O!", &PyArray_Type, &xval, &PyArray_Type, &yval, &PyArray_Type, &p0);
if (!parse_ind) {
PyErr_SetString(PyExc_StandardError, "Parsing of function arguments failed. Check function inputs.");
return NULL;
} else {
if (PyArray_TYPE(xval) != NPY_DOUBLE || PyArray_TYPE(yval) != NPY_DOUBLE || PyArray_TYPE(p0) != NPY_DOUBLE) {
PyErr_SetString(PyExc_TypeError, "Argument inputs are not of type \"double\".");
return NULL;
}
}
ndx = PyArray_NDIM(xval);
ndy = PyArray_NDIM(yval);
ndp = PyArray_NDIM(p0);
if (ndx != 1 || ndy != 1 || ndp != 1) {
PyErr_SetString(PyExc_AssertionError, "The dimension of the function input(s) not equal to 1");
return NULL;
}
dimx = PyArray_SHAPE(xval);
dimy = PyArray_SHAPE(yval);
dimp = PyArray_SHAPE(p0);
if (dimx[0] != dimy[0]) {
PyErr_SetString(PyExc_AssertionError, "The length of x and y vectors are not equal");
return NULL;
}
if (dimp[0] != 3) {
PyErr_SetString(PyExc_AssertionError, "Length of initial parameter vector not equal to 3.\
\nThe function being fitted takes 3 parameters.");
return NULL;
}
adata.xval = (double *) PyArray_DATA(xval);
x = (double *) PyArray_DATA(yval);
p = (double *) PyArray_DATA(p0);
ret = dlevmar_dif(lorentzfit, p, x, (int)dimp[0], (int)dimy[0], 100000, opts, info, NULL, NULL, (void *) &adata);
results = (PyArrayObject *) PyArray_SimpleNewFromData(1, dimp, NPY_DOUBLE, (void *) p);
return Py_BuildValue("(O,[d,d,i,i,i,i])",results, info[0], info[1], (int)info[5], (int)info[6], (int)info[7], (int)info[9]);
}
static PyMethodDef pylevmarmethods[] = {
{"levmarfit", levmarfit, METH_VARARGS, "Joel Vroom"},
{NULL, NULL, 0, NULL}
};
PyMODINIT_FUNC initpylevmar1(void) {
Py_InitModule("pylevmar1", pylevmarmethods);
import_array();
}
Granted, it is a lot of code for something you could easily do in Python but, in some cases, you are dealing with complicated models (eg. Heston's semi-analytical option pricing model) that simply take way too long in Python. When this code is compiled, you can use the resultant pylevmar1.pyd file as follows (see lines #3 and #34):import numpy as np
from scipy.optimize import leastsq
import matplotlib.pyplot as plt
import pylevmar1
np.random.seed(22)
def lorentz(p,x):
return p[2] / (1.0 + (x / p[0] - 1.0)**4 * p[1]**2)
def errorfunc(p,x,z):
return lorentz(p,x)-z
p = np.array([0.5, 0.25, 1.0], dtype=np.double)
x = np.linspace(-1.5, 2.5, num=30, endpoint=True)
noise = np.random.randn(30) * 0.05
z = lorentz(p,x)
noisyz = z + noise
p0 = np.array([-2.0, -4.0, 6.8], dtype=np.double) #Initial guess
##---------------------------------------------------------------------------##
## Scipy.optimize.leastsq
solp, ier = leastsq(errorfunc,
p0,
args=(x,noisyz),
Dfun=None,
full_output=False,
ftol=1e-15,
xtol=1e-15,
maxfev=100000,
epsfcn=1e-20,
factor=0.1)
##---------------------------------------------------------------------------##
## C++ Levmar
(sol, info) = pylevmar1.levmarfit(x, noisyz, p0)
##---------------------------------------------------------------------------##
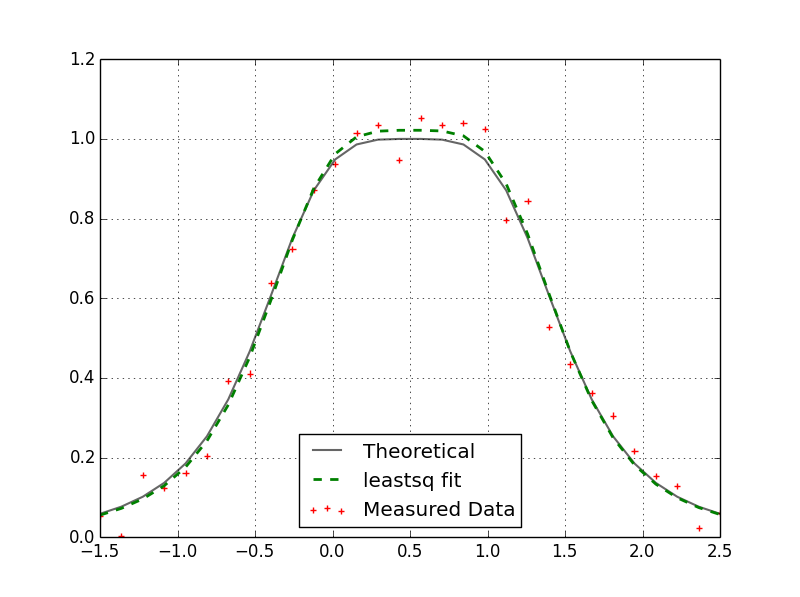
Here I am comparing my C++ levmar result with the scipy.optimize.leastsq result. Both results match and yield:
p = array([ 0.50708339, 0.26618568, 1.02169709])
When I throw these two routine's in a loop and execute them 10,000 times (with different noise) you can see the speed improvement (183x):
Scipy.optimize.leastsq runtime.....263.484s
C++ Levmar runtime........................1.439s