I haven't been all that impressed with the optimization routines included with
Scipy. They are too slow. I have been playing around with Manolis Lourakis' implementation of the
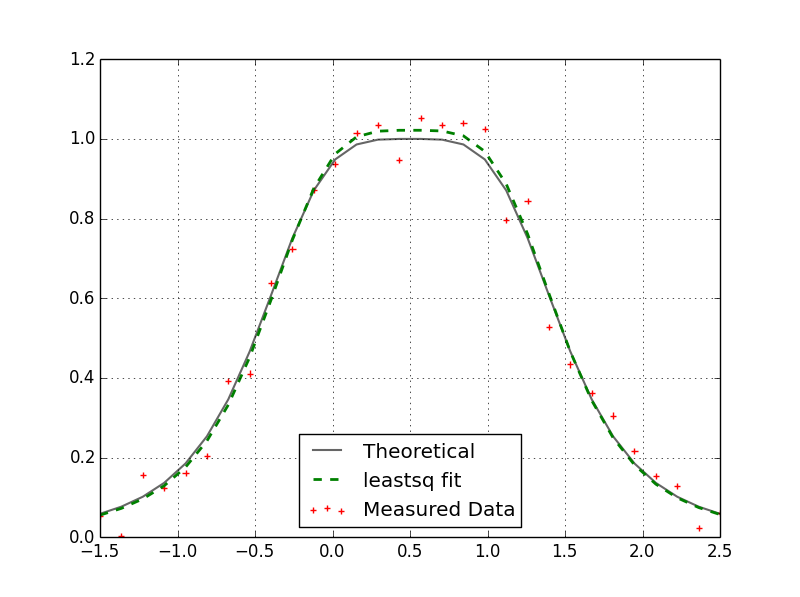
Levenberg-Marquardt algorithm (found here). It's taken me awhile but I finally figured out how to call this routine from Python. There is a Python interface for levmar called PyLevmar but I couldn't get that working. If you have a model written in Python that you are trying to fit to some measured data it is possible to use the C++ levmar routine but not recommended. Most of the routine's time is spent evaluating the function at various points (especially if you do not have an analytical expression for the Jacobian) and if it has to do this in Python you will see a marked slow down. So, while it will cost you some more development time, it is recommended to implement your model in C++ as well. I have taken a simple example here of the Lorentzian function. Suppose we have a bunch of measured values that we want to fit to a function of three parameters (parameter vector p). Our optimization routine should be able to give us the three parameters (p[0], p[1], and [2]) that best fit this data. Here is an example of such a fit:
To this end I created a Python module I can import into Python that will optimize this problem for us. From Python, I wanted to be able to send my initial guess of
p, my measured data, and the x-values these measurements were taken at and have returned the parameter values as well as the optimization information. To interface with C++ from Python, I made use of the
Numpy C-API. You can use Cython for this as well and it would probably be easier to implement but I haven't tried that yet. Using Microsoft's Visual Studio program I created a static library of the levmar routine in a separate project. I then reference that library in this DLL (pyd) module. My C++ code is as follows:
#include "Python.h"
#define NPY_NO_DEPRECATED_API NPY_1_7_API_VERSION
#include "arrayobject.h"
#include <iostream>
#include <iomanip>
#include <cmath>
#include <cfloat>
#include "levmar.h"
using namespace std;
struct argstruct {
double *xval;
};
double lorentz(double *p, double x) {
return p[2] / (1.0 + pow((x / p[0] - 1.0), 4) * pow(p[1], 2));
}
void lorentzfit(double *p, double *x, int m, int n, void *data) {
register int i;
struct argstruct *xp;
double xval;
xp = (struct argstruct *) data;
for(i=0; i<n i++) {
xval="xp-">xval[i];
x[i] = lorentz(p, xval);
}
}
static PyObject *levmarfit(PyObject *self, PyObject *args) {
PyArrayObject *xval, *yval, *p0, *results;
npy_intp *dimx, *dimy, *dimp;
argstruct adata;
int ndx, ndy, ndp, ret, parse_ind;
double *x, *p;
double opts[LM_OPTS_SZ] = {LM_INIT_MU, 1E-15, 1E-15, 1E-20, -LM_DIFF_DELTA};
double info[LM_INFO_SZ];
parse_ind = PyArg_ParseTuple(args, "O!O!O!", &PyArray_Type, &xval, &PyArray_Type, &yval, &PyArray_Type, &p0);
if (!parse_ind) {
PyErr_SetString(PyExc_StandardError, "Parsing of function arguments failed. Check function inputs.");
return NULL;
} else {
if (PyArray_TYPE(xval) != NPY_DOUBLE || PyArray_TYPE(yval) != NPY_DOUBLE || PyArray_TYPE(p0) != NPY_DOUBLE) {
PyErr_SetString(PyExc_TypeError, "Argument inputs are not of type \"double\".");
return NULL;
}
}
ndx = PyArray_NDIM(xval);
ndy = PyArray_NDIM(yval);
ndp = PyArray_NDIM(p0);
if (ndx != 1 || ndy != 1 || ndp != 1) {
PyErr_SetString(PyExc_AssertionError, "The dimension of the function input(s) not equal to 1");
return NULL;
}
dimx = PyArray_SHAPE(xval);
dimy = PyArray_SHAPE(yval);
dimp = PyArray_SHAPE(p0);
if (dimx[0] != dimy[0]) {
PyErr_SetString(PyExc_AssertionError, "The length of x and y vectors are not equal");
return NULL;
}
if (dimp[0] != 3) {
PyErr_SetString(PyExc_AssertionError, "Length of initial parameter vector not equal to 3.\
\nThe function being fitted takes 3 parameters.");
return NULL;
}
adata.xval = (double *) PyArray_DATA(xval);
x = (double *) PyArray_DATA(yval);
p = (double *) PyArray_DATA(p0);
ret = dlevmar_dif(lorentzfit, p, x, (int)dimp[0], (int)dimy[0], 100000, opts, info, NULL, NULL, (void *) &adata);
results = (PyArrayObject *) PyArray_SimpleNewFromData(1, dimp, NPY_DOUBLE, (void *) p);
return Py_BuildValue("(O,[d,d,i,i,i,i])",results, info[0], info[1], (int)info[5], (int)info[6], (int)info[7], (int)info[9]);
}
static PyMethodDef pylevmarmethods[] = {
{"levmarfit", levmarfit, METH_VARARGS, "Joel Vroom"},
{NULL, NULL, 0, NULL}
};
PyMODINIT_FUNC initpylevmar1(void) {
Py_InitModule("pylevmar1", pylevmarmethods);
import_array();
}
Granted, it is a lot of code for something you could easily do in Python but, in some cases, you are dealing with complicated models (eg. Heston's semi-analytical option pricing model) that simply take way too long in Python. When this code is compiled, you can use the resultant pylevmar1.pyd file as follows (see lines #3 and #34):
import numpy as np
from scipy.optimize import leastsq
import matplotlib.pyplot as plt
import pylevmar1
np.random.seed(22)
def lorentz(p,x):
return p[2] / (1.0 + (x / p[0] - 1.0)**4 * p[1]**2)
def errorfunc(p,x,z):
return lorentz(p,x)-z
p = np.array([0.5, 0.25, 1.0], dtype=np.double)
x = np.linspace(-1.5, 2.5, num=30, endpoint=True)
noise = np.random.randn(30) * 0.05
z = lorentz(p,x)
noisyz = z + noise
p0 = np.array([-2.0, -4.0, 6.8], dtype=np.double) #Initial guess
##---------------------------------------------------------------------------##
## Scipy.optimize.leastsq
solp, ier = leastsq(errorfunc,
p0,
args=(x,noisyz),
Dfun=None,
full_output=False,
ftol=1e-15,
xtol=1e-15,
maxfev=100000,
epsfcn=1e-20,
factor=0.1)
##---------------------------------------------------------------------------##
## C++ Levmar
(sol, info) = pylevmar1.levmarfit(x, noisyz, p0)
##---------------------------------------------------------------------------##
Here I am comparing my C++ levmar result with the scipy.optimize.leastsq result. Both results match and yield:
p = array([ 0.50708339, 0.26618568, 1.02169709])
When I throw these two routine's in a loop and execute them 10,000 times (with different noise) you can see the speed improvement (
183x):
Scipy.optimize.leastsq runtime.....263.484s
C++ Levmar runtime........................1.439s